1 Даны два действительных числа a и b. Получить их сумму, разность и произведение.
2 Даны действительные числа x и y. Получить
4 Даны два действительных положительных числа. Найти среднее арифметическое и среднее геометрическое этих чисел.
5 Даны два действительных числа. Найти среднее арифметическое этих чисел и среднее геометрическое их модулей. (*)
6 Даны катеты прямоугольного треугольника. Найти его гипотенузу и площадь.
7 Смешано V1 литров воды температуры t1 с V2 литрами воды температуры t2. Найти объём и температуру образовавшейся смеси.
8 Определить периметр правильного n-угольника, описанного около окружности радиуса r.
9 Три сопротивления R1, R2, R3 соединены параллельно. Найти сопротивление соединения.
10 Определить время падения камня на поверхности земли с высоты h.
11 Даны x, y, z. Вычислить a, b, если
12 Дана сторона равностороннего треугольника. Найти площадь этого треугольника.
13 Вычислить период колебания маятника длины L.
14 Определить силу притяжения F между телами массы m 1 и m2 , находящимся на расстоянии r друг от друга.
15 Даны гипотенуза и катет прямоугольного треугольника. Найти второй катет и радиус вписанной окружности.
16 Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.
17 Найти площадь кольца, внутренний радиус которого равен 20, а внешний - заданному числу r (r>20).
18 Треугольник задан величинами своих углов и радиусом описанной окружности. Найти стороны треугольника.
19 Определить время, через которое встретятся два тела, равноускоренно движущиеся навстречу друг другу, если известны их начальные скорости, ускорения и начальное расстояние между ними.
20 Найти сумму членов арифметической прогрессии a, a+d, ..., a+(n-1)d по данным значениям a, d, n.
21 Даны действительные числа c,d. Вычислить
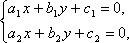
где x1 - больший, а x2 - меньший корни уравнения x2 - 3x - |cd| = 0
22 Найти площадь равнобочной трапеции с основаниями a и b и углом α при большем основании a.
23 Треугольник задан длинами сторон. Найти:
24 Вычислить расстояние между двумя точками с координатами x1, y1 и x2, y2.
25 Треугольник задан координатами своих вершин. Найти:
26 Найти площадь сектора, радиус которого равен 13.7, а дуга содержит заданное число радиан φ.
27 Даны действительные положительные числа a, b, c. По трем сторонам с длинами a, b, c можно построить треугольник. Найти углы треугольника.
28 Дано действительное число X. Не пользуясь никакими другими арифметическими операциями, кроме умножения, сложения и вычитания, вычислить 2x4-3x3+4x2-5x+6. Разрешается использовать не более четырёх умножений и четырёх сложений и вычитаний.
29 Даны действительные числа x, y. Не пользуясь никакими другими операциями, кроме умножения, сложения и вычитания, вычислить
3x2y2 - 2xy2 - 7x2y - 4y2 + 15xy + 2x2 - 3x + 10y + 6. Разрешается использовать не более восьми умножений и восьми сложений и вычитаний.
30 Дано действительное число X. Не пользуясь никакими другими операциями, кроме умножения, сложения и вычитания, вычислить
1 - 2x + 3x2 - 4x3 и 1 + 2x + 3x2 + 4x3. Разрешается использовать не более восьми операций.
31 Дано действительное число a. Не пользуясь никакими другими арифметическими операциями, кроме умножения, получить:
32 Дано действительное число a. Не пользуясь никакими другими арифметическими операциями, кроме умножения, получить:
2 Даны действительные числа x и y. Получить
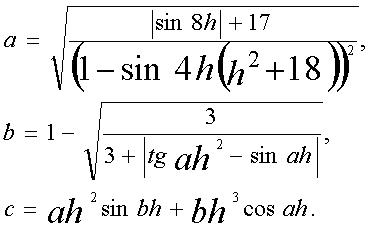
4 Даны два действительных положительных числа. Найти среднее арифметическое и среднее геометрическое этих чисел.
5 Даны два действительных числа. Найти среднее арифметическое этих чисел и среднее геометрическое их модулей. (*)
6 Даны катеты прямоугольного треугольника. Найти его гипотенузу и площадь.
7 Смешано V1 литров воды температуры t1 с V2 литрами воды температуры t2. Найти объём и температуру образовавшейся смеси.
8 Определить периметр правильного n-угольника, описанного около окружности радиуса r.
9 Три сопротивления R1, R2, R3 соединены параллельно. Найти сопротивление соединения.
10 Определить время падения камня на поверхности земли с высоты h.
11 Даны x, y, z. Вычислить a, b, если
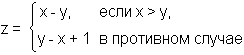
12 Дана сторона равностороннего треугольника. Найти площадь этого треугольника.
13 Вычислить период колебания маятника длины L.
14 Определить силу притяжения F между телами массы m 1 и m2 , находящимся на расстоянии r друг от друга.
15 Даны гипотенуза и катет прямоугольного треугольника. Найти второй катет и радиус вписанной окружности.
16 Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.
17 Найти площадь кольца, внутренний радиус которого равен 20, а внешний - заданному числу r (r>20).
18 Треугольник задан величинами своих углов и радиусом описанной окружности. Найти стороны треугольника.
19 Определить время, через которое встретятся два тела, равноускоренно движущиеся навстречу друг другу, если известны их начальные скорости, ускорения и начальное расстояние между ними.
20 Найти сумму членов арифметической прогрессии a, a+d, ..., a+(n-1)d по данным значениям a, d, n.
21 Даны действительные числа c,d. Вычислить
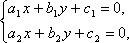
где x1 - больший, а x2 - меньший корни уравнения x2 - 3x - |cd| = 0
22 Найти площадь равнобочной трапеции с основаниями a и b и углом α при большем основании a.
23 Треугольник задан длинами сторон. Найти:
-
а) длины высот;
б) длины медиан;
в) длины биссектрис;
г) радиусы вписанной и описанной окружностей.
24 Вычислить расстояние между двумя точками с координатами x1, y1 и x2, y2.
25 Треугольник задан координатами своих вершин. Найти:
-
а) периметр треугольника;
б) площадь треугольника;
26 Найти площадь сектора, радиус которого равен 13.7, а дуга содержит заданное число радиан φ.
27 Даны действительные положительные числа a, b, c. По трем сторонам с длинами a, b, c можно построить треугольник. Найти углы треугольника.
28 Дано действительное число X. Не пользуясь никакими другими арифметическими операциями, кроме умножения, сложения и вычитания, вычислить 2x4-3x3+4x2-5x+6. Разрешается использовать не более четырёх умножений и четырёх сложений и вычитаний.
29 Даны действительные числа x, y. Не пользуясь никакими другими операциями, кроме умножения, сложения и вычитания, вычислить
3x2y2 - 2xy2 - 7x2y - 4y2 + 15xy + 2x2 - 3x + 10y + 6. Разрешается использовать не более восьми умножений и восьми сложений и вычитаний.
30 Дано действительное число X. Не пользуясь никакими другими операциями, кроме умножения, сложения и вычитания, вычислить
1 - 2x + 3x2 - 4x3 и 1 + 2x + 3x2 + 4x3. Разрешается использовать не более восьми операций.
31 Дано действительное число a. Не пользуясь никакими другими арифметическими операциями, кроме умножения, получить:
-
а) a4 за две операции;
б) a6 за три операции;
в) a7 за четыре операции;
г) a8 за три операции;
д) a9 за четыре операции;
е) a10 за четыре операции;
ж) a13 за пять операций;
з) a15 за пять операций;
и) a21 за шесть операций;
к) a28 за шесть операций;
л) a64 за шесть операций.
32 Дано действительное число a. Не пользуясь никакими другими арифметическими операциями, кроме умножения, получить:
-
а) a3 и a10 за четыре операции;
б) a4 и a20 за пять операции;
в) a5 и a13 за пять операции;
г) a5 и a19 за пять операции;
д) a2, a5 и a17 за шесть операции;
е) a4, a12 и a28 за шесть операции.
(*) См. также неравенство о среднем квадратическом, арифметическом, геометрическом и гармоническом:
\( \bar x_{квадратич.} \geq \bar x_{арифм.} \geq \bar x_{геом.} \geq \bar x_{гармонич.} \)
